Deborah R. Fowler
Wobble Wheels
Posted May 28 2023keywords: dot product, wrangle, vex, iteration, detail function
Created in Houdini 19.5.303 LC using a dot product similar to my example for the "Dot Product Follow"
Also on youtube at https://www.youtube.com/shorts/3Dav0Bot2ck
The solution to the problem is directly a result of the dot product. Given two vectors defined by two points (these can be in any direction, I created one with z being my horizontal and y being my vertical) z0,y0 and z1,y1 find the angle
In this situation, the box is pivoting from a value that is (0,-.2,0) so I can use that as my (0,-.2) and my z0,y0 for my calculations.
Below in the comments you will see the two vectors defined and a simple dot product to find the resulting angle:
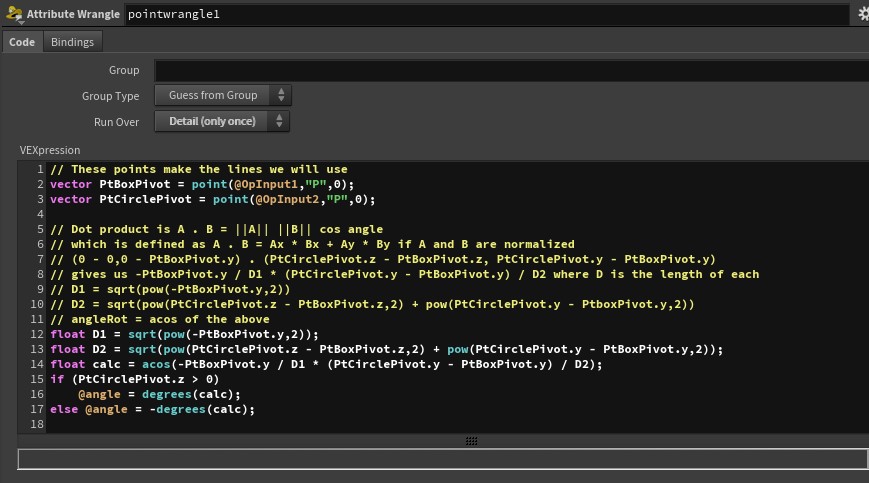
Note that anytime you need to do calculations you can use a wrangle node. It does not have to be attached in the network, just referenced by it.
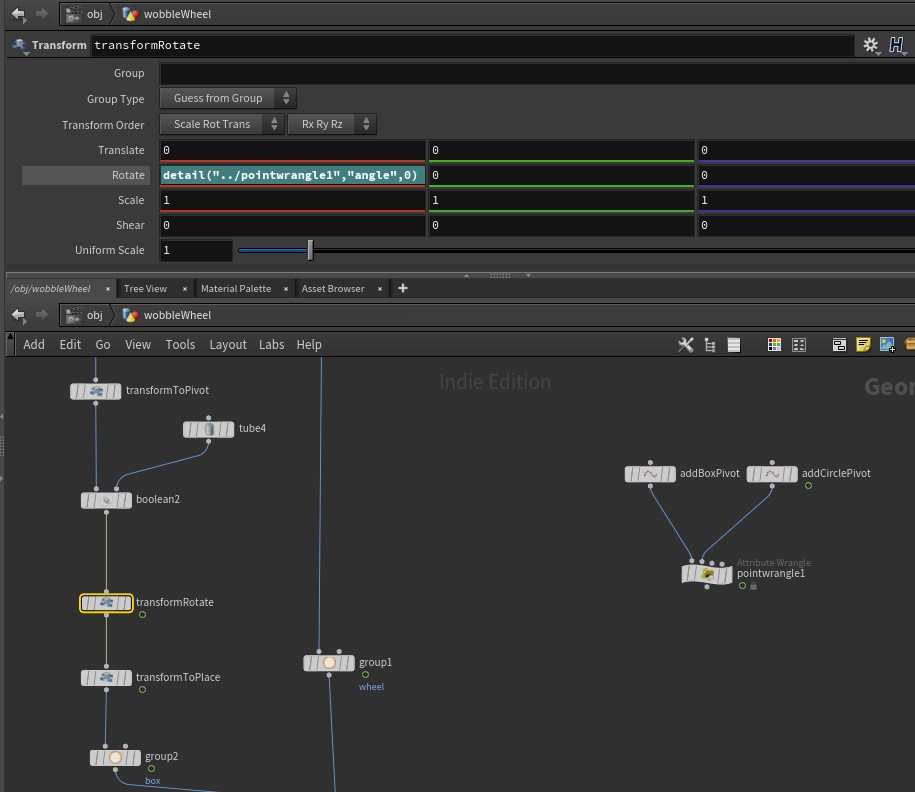
I prefer the method of transforming my geometry to the Pivot (transformToPivot) so that I can physically see what I am doing. You can also move pivot points.
Then transformRotate references the pointwrangle1 node with the code to easily calculate the dot product between the vectors.
Finally transformToPlace puts the geometry in the position that you want it to be in.
I also added some randomness to the row of wobble wheels by using a timeshift node and accessing the "copy number" or "iteration" number by using a detail function to retreive it from the for-each "meta" node.
